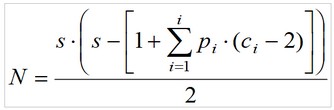DÉNOMBREMENT DES DIAGONALES INTÉRIEURES DES POLYÈDRES CONVEXES
Élaboration d’une relation entre le type de polyèdre et le nombre des diagonales intérieures

1. REMARQUES
C’est en janvier 1999 que l’idée m’est venue de m’intéresser au dénombrement des diagonales intérieures des polyèdres, lors du traitement d’un chapitre consacré aux solides avec mes élèves de 9ème.
Cette démarche est personnelle mais pourrait très bien faire l’objet d’un travail dans le cadre de leçons de math appliquées.
Quelques références utiles pour la démarche :
Polyèdres (théorie) : https://xavier.hubaut.info/coursmath/3di/polyed.htm, Xavier Hubaut 1995-2004
Polyèdres (animations Flash) : http://www.sciences.univ-nantes.fr/sites/genevieve_tulloue/Polyedres/Platon/ronde.html
Polyèdres (théorie Mathcurve): https://mathcurve.com/polyedres/polyedres.shtml
Une balade dans le monde des polyèdres (Java) : http://www.ac-noumea.nc/maths/amc/polyhedr/
Poly Pro 1.12 (gratuiciel) : http://www.peda.com/
2. HYPOTHÈSE
Dans le cadre de l’étude des solides, l’idée de cette démarche est de démontrer l’hypothèse suivante :
Il existe une relation entre le nombre de diagonales intérieures*) de tout polyèdre convexe et ses caractéristiques propres qui sont :
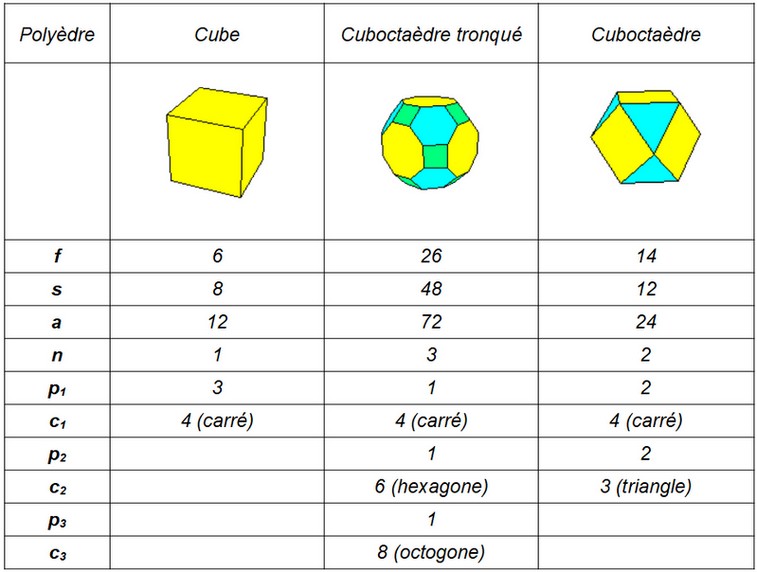
f – le nombre de faces (polygones)
s – le nombre de sommets du polyèdre
a – le nombre d’arêtes du polyèdre
n – nombre de polygones différents constituant les faces
pi – nombre de polygones identiques auxquels appartient un sommet.
ci – le nombre de côtés des polygones auxquels appartient un sommet.
Les divers exemples ci-dessous illustrent les différentes caractéristiques qui se déterminent à partir de n’importe quel sommet du polyèdre :
*) Une diagonale est dite « intérieure » si elle n’appartient pas aux faces du polyèdre.
Le nombre de diagonales (N) dépend du nombre de sommets utiles ou possibilités (d). C’est en fait l’ensemble des sommets qui, avec le sommet de référence, permettent de tracer une diagonale intérieure. Cela représente finalement le nombre de diagonales intérieures partant de chaque sommet.
Le nombre (N) total de diagonales intérieures du polyèdre est finalement le suivant :

Cela signifie que si de chaque sommet du polyèdre il part d diagonales intérieures, le nombre total de diagonales intérieures N est égal à la moitié du produit de s par d, vu qu’une paire de sommets n’engendrent qu’une seule et unique diagonale intérieure.
Si s est aisément déterminé, d nécessite une réflexion plus poussée.
3. DÉTERMINATION DE d, POSSIBILITÉS DE CHAQUE SOMMET.
▪ d dépend des caractéristiques du polyèdre.
▪ d dépend directement du nombre (z) de sommets stériles. Un sommet est dit stérile par rapport au sommet de référence s’ils appartiennent tous les deux au même polygone (face du polyèdre).
▪ d dépend donc directement du nombre de faces (n) auxquelles appartient le sommet de référence.
▪ d dépend également du nombre de polygones (pi) identiques auxquels appartient le sommet de référence.
▪ d dépend aussi du nombre de côtés (ci) des polygones auxquels appartient le sommet de référence.
Je n’ai pas trouvé de polyèdres ou un sommet appartient à plus de trois faces différentes.
▪ d dépend de (s), le nombre de sommets du polyèdre.
▪ d dépend des groupes de polygones constituant les faces auxquelles appartient le sommet de référence (pi).
▪ Une diagonale intérieure est impossible entre deux sommets appartenant à une même face
▪ Le calcul du nombre (z) de sommets stériles pour chaque groupe de polygones se calcule ainsi :
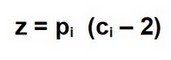
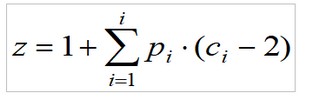
L’unité ajoutée représente le sommet de référence qu’il ne faut pas oublier.
Finalement, on obtient d, le nombre de sommets utiles ou possibilités, en soustrayant z à s :
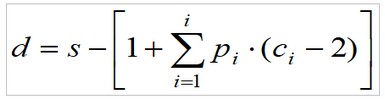
4. Conclusions.
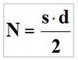
Donc :